同态加密

20世纪70年代末，就在RSA公钥密码体制公布的第二年，Ron Rivest、Len Adleman和Michael Dertouzos 发表了题为《论数据库与隐私同态》的报告。文中详细介绍了金融公司如何运用云提供商（当时叫做“商用分时服务”）存储和计算加密数据，从此，密码学里一个新的名词术语“同态加密”诞生了。直到2009年IBM的Craig Gentry首次提出了一种基于理想格的全同态算法，同态加密从概念到理论得到进一步完善，也逐渐有了工程实现。

举个例子

爱丽丝是一家珠宝店老板，打算让员工将一块黄金打造成首饰，但是担心工人会在打造过程中偷取黄金，于是她制造了一个带锁的箱子，用来存放黄金和做好的首饰，钥匙由她随身保管。通过手套箱工人可以将手伸入箱子加工首饰，但无法拿到黄金和首饰。而爱丽丝则可以通过钥匙向手套箱添加原料，并取出加工好的首饰。

• 爱丽丝：数据拥有者
• 黄金：原始数据
• 手套箱：加密算法；
• 钥匙和锁：用户密钥；
• 通过钥匙向手套箱添加原料：将数据用同态加密方式进行加密；
• 员工加工首饰：应用同态特性，在无法取得数据的条件下直接对加密结果进行处理；
• 取出加工好的首饰：对结果进行解密，直接得到处理后的结果

用符号表示如下：

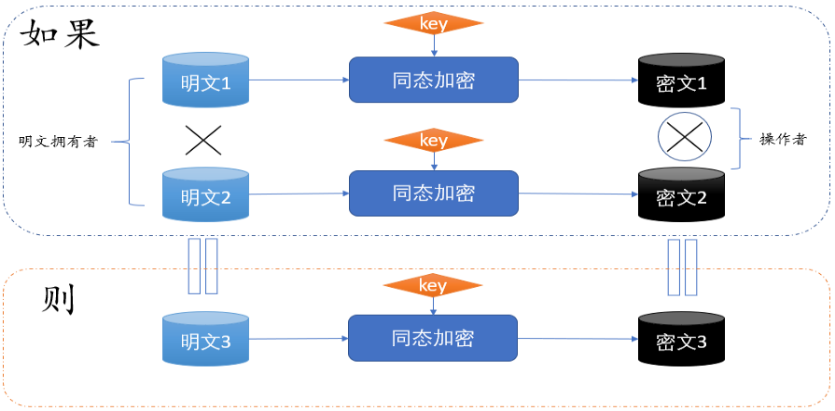
简单来说就是，明文的互操作何以转换成密文的互操作。

比如，上图中，密文1和密文2分别是明文1和明文2经过加密后的对应的密文，明文1和明文2相乘得到明文3，对密文3解密，得到的结果等于明文1乘以明文2，如果此加密算法具有这样的特性，那么就说明此算法具有乘法同态性。

或乘法同态，“全同态加密”既能实现加法同态又能实现乘法同态（其他运算都可以通过加法和乘法实现）

RSA乘法同态举例介绍

RSA是计算机通信安全的基石，是一种公钥加密算法（加密密钥和解密密钥不是同一个），在这里通过例子简要证明RSA具有乘法同态性，即两明文数字（T1、T2）用公钥加密后得到的两个密文（C1、C2），将密文乘积（C1×C2）用私钥解密，如果解密结果等于两明文之积（T1×T2），则RSA具有乘法同态性，如下：

一、构造密钥对：

1. 随机选择两个不相等的质数 p=3和q=5（实际应用中，这两个质数越大，就越难破解，这里选择两个小数只是为说明原理）
2. 计算p和q的乘积n=15（ n的长度就是密钥长度，15二进制是1111，一共有4位，所以这个密钥就是4位。实际应用中，RSA密钥一般是1024位，重要场合则为2048位。也就是21024-22048，约为10308-10616）
3. 计算n的欧拉函数φ(n)=(p-1)(q-1)=8
4. 随机选择一个整数e，条件是1< e < φ(n)，且e与φ(n) 互质，在这里选e=3（实际应用中，常常选择65537。）

5. 计算e对于φ(n)的模反元素d=11（所谓“模反元素”就是指有一个整数d，可以使得ed被φ(n)除的余数为1。

   ed ≡ 1 (mod φ(n))；

   这个式子等价于

   ed - 1 = kφ(n)；

   于是，找到模反元素d实质上就是对下面这个二元一次方程求解。

   ex + φ(n)y = 1

   已知 e=3, φ(n)=8，

   3x + 8y = 1

   这个方程可以用“扩展欧几里得算法”求解，此处省略具体过程，在这里算出一组解（11，-4）即d=11）

6. 将n和e封装成公钥，n和d封装成私钥即 公钥（15,3），私钥（15,11）

二、加解密运算：

1. 随机选取两个数字T1=2和T2=3进行加密运算分别得到密文：

   （ 明文T1、T2必须是整数（字符串可以取ascii值或unicode值），且必须小于n，所谓“加密”，就是算出下式的c， te ≡ c (mod n)）

   C1= 23mod（15）=8

   C2= 33mod（15）=12

2. 对（ C1×C2 ）做解密运算得（所谓解密即算出cd ≡ t (mod n)中对应的t）

   t= （C1×C2）d mod（n）= 9611mod（15）=6；

   又T1×T2=6；

   由此可见RSA具有乘法同态性，两个密文之积的解密结果等于明文之积即：

   decrypt（C1×C2）≡ T1×T2